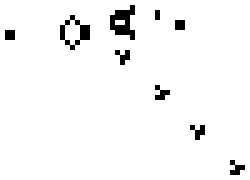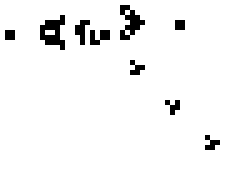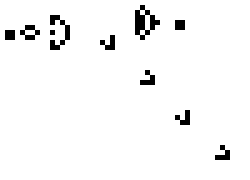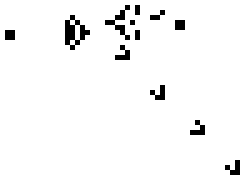用自动机可以模拟出一个世界，虽然这个世界是虚拟的，但这个世界里面将会根据基础的自动机规则自动推算出很多有趣的规则。在当前的世界里面可以认定光速是最快的，在自动机世界里面也可以认定为有某个东西是具备最快速度，同时如果这个自动机世界里面存在智慧生物那么他将很难猜到自动机的创建规则以及他认为具备最快速度的东西的本质是什么，本文基于一个假定的自动机世界，通过简单的语言告诉大家在自动机里面的光速是什么同时告诉大家这个最快速度对自动机世界的意义

我不是物理学家，本文也是不是任何证明现实世界光速相关的文章。但我是计算机的砖家，搬了很多年的砖也知道在计算机里面可以简单做出一个世界，本文就是说明光速带的信息很难反过来知道世界的规则。而如果知道世界的简单规则就可以推出很多复杂的规则

从我的上篇博客自动机告诉了大家如何创建一个自动机的世界，以下为一个创建自动机世界的方法，创建规则如下

• 在一个有限的二维布尔数组里面，以 true 代表存活
• 不断根据算法规则遍历数组，同时创建出新的相同大小的数组用于迭代
• 新创建的数组将根据旧数组的数据按照一定的算法更新数组每个元素的值

从上层看，可以认为我有一个数组，但这个数组的元素会跟随时间进行变化。虽然底层说的是使用两个数组，但实际上可以从上层上看到的只有一个数组，因为新创建的数组就替换旧的数组。将数组作为一张图片，每个元素具有固定的宽度和高度，里面的元素按照布尔值给不同的颜色，就可以画出自动机的世界，这是一个二维的世界

那么新数组创建的算法可以怎么选？下面是一个简单的计算方法，设定每次更新新数组就成为新的回合开始，每个数组里面的元素称为 Cell 而根据布尔值状态可以认定为 Cell 的存活或不存活，那么创建自动机世界只需要三条规则

• 在 Cell 周围有两个或三个邻居存活，他就可以存活。这里的周围指的是将二维数组放在二维平面对应的元素的周围的元素
• 如果 Cell 已经不存活，但他周围有三个邻居，于是他就可以出生
• 在 Cell 周围，如果有超过三个以上的邻居，他就因为太拥挤而不存活。如果有小于两个邻居存活，他因为他孤单而不存活

简单按照颜色黑色和白色，同时每个格子表示一个数组的元素，那么运行自动机世界可以看到下图

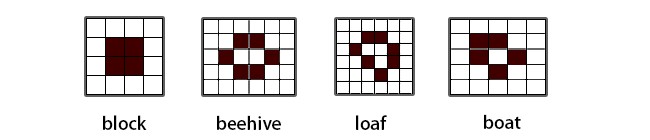
上面是刚好满足以上条件 1 的静态图，也就是随着数组的迭代也就是回合数的变化，这些自动机世界里面的图案是不会发生更改的。但下面的图片将会随着回合数的变化，进行循环变化

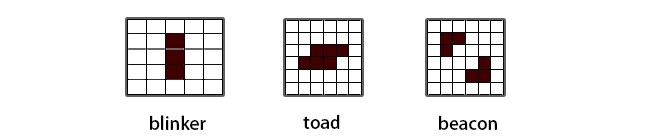
再复杂一点就是周期比较长的，可以认为是某个在自动机里面的小生物的图案

一些复杂的生物

在这个自动机世界里面有一个图案能够按照一定的方向不断运动，我称这个图案为逃逸，也就是在一个无限大的二维空间里面，如果这是一片除了逃逸之外就没有其他 Cell 的空间，那么逃逸将会无限向一个方向运动

例如下面图案将会不断创建逃逸让他向右下角运动

按照光锥的说法，假定在自动机里面的某个生物想要知道这个世界发生了什么，他首先应该需要收到对应的消息，假定他收到的消息就是逃逸这个图案，那么请问我在上面图案存在多久之后，在距离这个图案一定距离的生物才能知道上面图案的存在。也就是最短的事件就是逃逸运动的时间，在自动机里面的生物将无法知道在逃逸运动时间之外的其他事件，也就是当有某个图案存在的时候，需要等待这个图案发送的逃逸到达生物的时候，生物才能知道某个图案的存在

按照二维数组的刷新就可以定义出自动机里面的最小时间单位，只是自动机的回合和现实的时间其实可以没有任何对应，但根据自动机里面最小的时间就可以知道自动机里面的逃逸的最快速度是多少

换句话就是自动机里面的最快速度就取决于自动机世界的定义，按照自动机世界的定义，每个 Cell 只会影响到周围的 Cell 而不会在下一回合影响到距离他更远的元素。而根据光锥的说法，在最快速度的东西带的信息到达之前是无法知道事件的发生，也就是在自动机世界已经规定了一个世界局部范围

假定在自动机里面的某个生物，或由很多生物构成的社会只能存在一定的时间，毕竟是在计算机创建出这个世界，万一我就想运行一分钟之后就关机了，这也就决定了这个自动机世界能运行的回合数是有限的

那么根据上文的说法，在某个由很多生物构成的社会已经存在一些先知的图案，同时这些先知能够根据到达的逃逸拿到对应的信息从而期望能知道先知他所在的世界是什么，或者这个世界正在发生什么。可惜如果在这个社会能存在的一定时间之内，还有更远处的逃逸无法到达这个社会，那么在社会里面的先知也是无法知道更远的事件。也就是按照逃逸的速度就可以将自动机世界划分为多个局部，虽然在相同的二维数组上存在，但并不会存在任何的影响

从简单的自动机世界就可以知道，在了解世界的创建规则的时候就可以明白在这个世界里面的具有最快速度的东西是什么从而反过来推算出某个文明的边界

在自动机里面的生物是很难知道他所在的世界其实是计算机模拟的，同时也很难知道他所在的世界的规则。同时更难的是做到预知未来，在一个复杂的自动机里面是不存在任何数学公式可以做到一次计算到某个回合的状态，而是需要一个回合一个回合计算下去。也就是在一个个回合计算的过程中就相当于自动机世界在迭代。例如我创建了初始化的二维数组作为世界，然后如果我在计算机外想要知道在第100回合的自动机世界的数组，那么我只能通过计算第二回合发生了什么然后计算第三回合的数组，在我计算的过程就可以认为这个自动机世界的时间已经在走了，在我知道了第一百个回合的时候其实自动机世界也到了第一百个回合

在计算机之外的我可以知道整个数组的状态都是这样，更不要说如果在自动机里面的生物可以怎么做，首先自动机里面的生物如果造出来计算机，那么他的计算机本身就在世界里面，也就是无法有更大的算力可以计算出他所在这个世界数组的未来确定的数组

反过来假设现实世界也是一个自动机，那么如何能知道自动机的规则以及知道整个世界